
Olga Paris-romaskevich
I am currently a post-doc at IRMAR in the University of Rennes I.
I work in dynamical systems, ergodic theory and geometry. Currently, I am focused on algebraic dynamical systems of zero entropy and on tiling billiards.
I invite you to check out the French version of this site for more information (especially on popularisation, teaching and upcoming events) ! The English version of the site is updated for research.
Contact
olga.romaskevich at univ-rennes1.fr
IRMAR, Campus de Beaulieu, bâtiments 22 et 23
263 avenue du Général Leclerc, CS 74205
35042 RENNES
bureau : 434
07 68 56 36 88
écrivez-moi
Research
My previous work mostly concentrated on the understanding of mathematical models of systems coming from physics and mechanics. I worked in the setting of hyperbolic systems, and ergodicity. Currently I am concentrated on the systems which, in some sense, live on the other edge of mathematical world : zero entropy systems. I am studying integrable behaviour of dynamical systems, billiards in tilings, and working on the concept of polynomial entropy (the complexity measure that can be positive when the entropy is zero).
Here is the list of my publications and pre-prints, rearranged by theme.
Publications and preprints
Consider a periodic tiling of a plane by congruent triangles which is
obtained from an equilateral tiling by some linear transformation. We study a billiard in this tiling defined in a following way. A ball follows straight line segments and bounces from the boundaries of the tiles into neighbouring tiles in such a way that the coefficient of refraction is equal to -1. We show that almost all the trajectories of such a tiling exhibit integrable behaviour : they are either closed or linearly escaping. Although an exceptional family of trajectories has a very different, non-integrable behavior. These trajectories approach Rauzy-like fractals. We give a more precise description
of these exceptional trajectories. The proofs use the connection of this system with the dynamics of interval exchange transformations with flips. We also give the generalizations of our results to quadrilateral tilings.
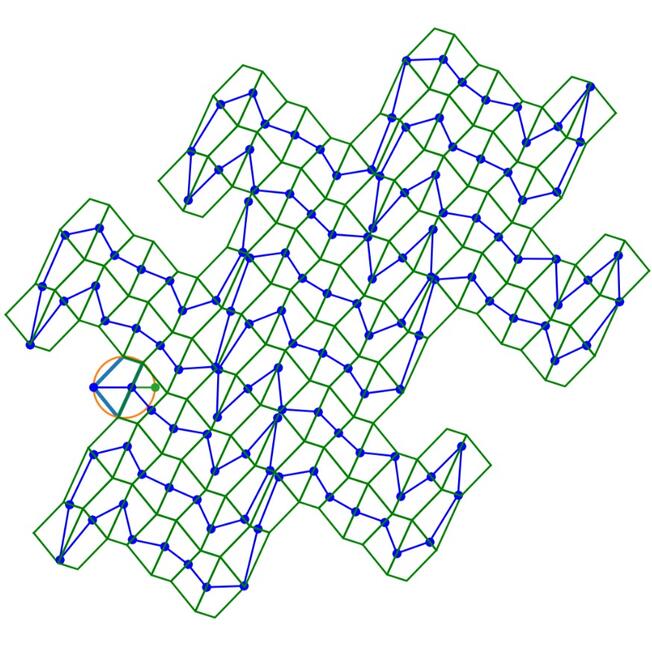
[7] P. Hubert, O. Paris-Romaskevich Triangle tilling billiards draw fractals only if aimed at the circumcenter, preprint // arxiv:1804.00181
We study the behaviour of a swivelling arm on the hyperbolic plane and find out an explicit formula for its angular velocity in the case when the angular velocities of each arm are rationally independent (in the ergodic setting). This work generalises a classical result of P. Hartman, E. Van Kampen, A. Wintner and H.Weyl for the study of a swivelling arm on the euclidian plane.
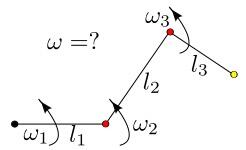
[6] O. Romaskevich Epicycles in hyperbolic sky, preprint // arxiv: 1704.01339
We give a normal form for a Hölder hyperbolic skew product in the neighbourhood of a fixed point. This normal form is smooth with respect to the coordinate on the fiber and Hölder with respect to the base. This theorem inscribes in the quest of understanding the generic behaviour of normally hyperbolic foliations.
[5] Yu. Ilyashenko, O. Romaskevich Sternberg linearization theorem for skew products, Journal of Dynamical and Control Systems, Volume 22, Issue 3, pp. 595-614 (2016) // arxiv: 1505.05776 // journal version
We prove a theorem for the mean convergence of markovian spherical averages for measure-preserving actions of the free group. The theorem is proven for an open set of matrices governing the Markov chain . The Markov graph has to contain some specific graph as a subgraph. This theorem gives us the techniques to think about the convergence about spherical averages for Gromov hyperbolic groups.
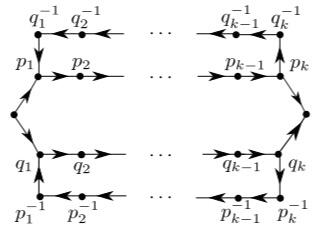
[4] L.Bowen, A.Bufetov, O. Romaskevich, Mean convergence of Markovian spherical averages for measure-preserving actions of the free group, Geometriae Dedicata, 181 (1), 293-306, (2015) // arxiv: 1502.01797 // journal version
The centers of inscribed circles of triangles corresponding to triangular orbits of an elliptic billiard belong to an ellipse. The proof of this theorem is based on classical ideas of projective geometry as well as on the modern approach to the complexification of reflection law.
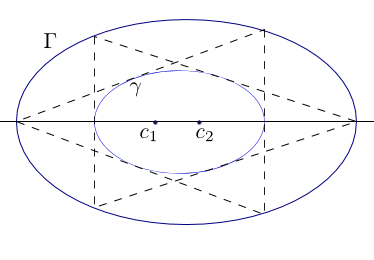
[3] O. Romaskevich, On the incenters of triangular orbits on elliptic billiards, L’Enseignement Mathématique (2) 60 (2014), 247–255 // arxiv: 1304.7588// journal version
In these two articles we study a three-parametric family of vector fields on the torus that models the behaviour of Josephson junctions. The first-return map on a meridian of the torus has Arnold tongues (level sets of rotation number with non-empty interior) with a very interesting structure. First, they exist for only integer (and not rational) values of rotation number and second, their boundaries auto-intersect. We describe the behaviour of these tongues in different limiting regimes.
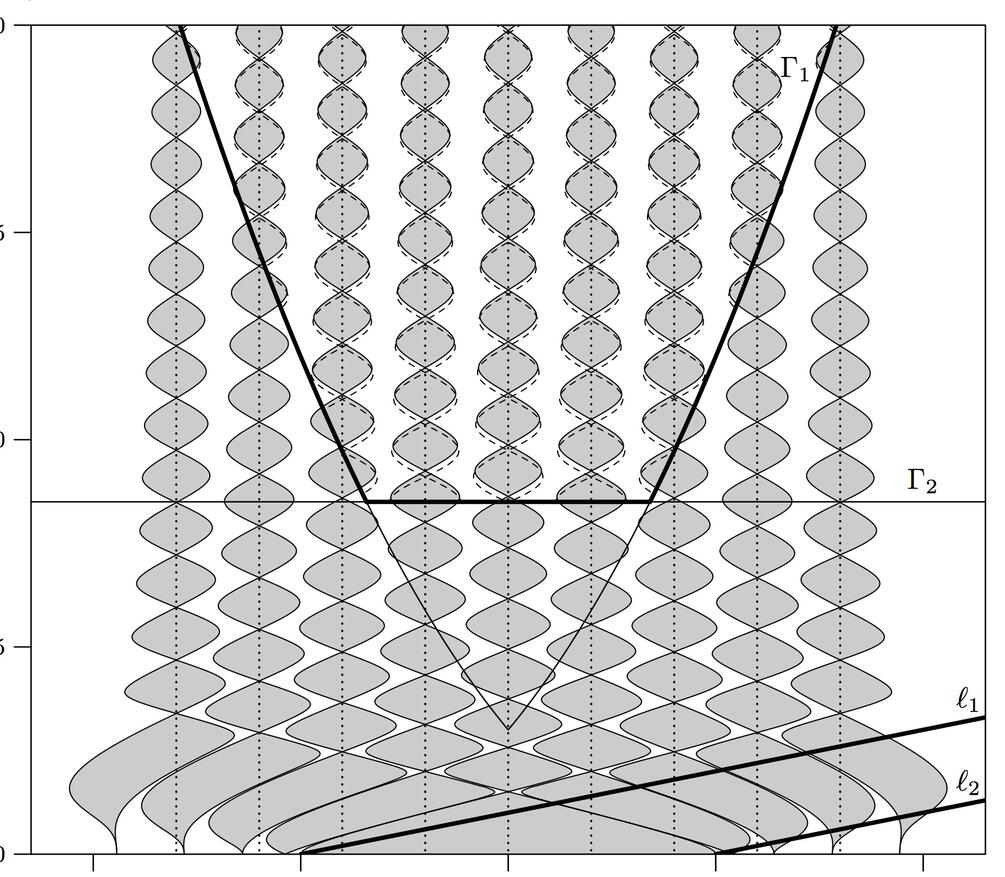
[2] A. Klimenko, O. Romaskevich , Asymptotic properties of Arnold tongues and Josephson effect, Moscow Mathematical Journal, volume 14, issue 2, pp. 367-384, (2014), // arxiv: 1305.6746 // journal version
[1] V. Kleptsyn, I. Schurov, O. Romaskevich Josephson effect and slow-fast systems (in Russian), Nanostructures. Mathematical physics and modelling, 8:1, pp. 31–46, (2013); // arxiv: 1305.6755 // journal version
Thèse
Dynamics of physical systems, normal forms and Markov chains
My thesis was written under supervision of Étienne Ghys and Yulij Ilyashenko, in-between Russia and France. This great experience is called thèse en co-tutelle in French. I had two defenses in 2016: on the 25th of October in Russia and on the 7th December in France.
I am кандидат наук and docteur en mathématiques.
Please contact me if you are interested in a complete .pdf version of my thesis (available in English with French introduction as well as in Russian).
Curriculum Vitae
Initial coordinates in space-time
born 6th July 1990 in Moscow, nationality: Russian
employment
october 2017 - now postdoc at IRMAR, Université de Renes I
2016-2017 ATER at Unité des Mathématiques Pures et Appliquées, ENS de Lyon
Studies
2003-2007 Moscow School 57 (silver medal)
2007-2012 undergraduate studies: faculty of mathematics and mechanics of Moscow State University (diploma with honours in 2012)
2012-2016 graduate student on co-tutelle program between National Research University Higher School of Economics and École Normale Supérieure de Lyon (under supervision of Étienne Ghys and Yulij Ilyashenko)
PRIze
2016 Bourse l'Oréal-UNESCO for Women in Science
co-organized events
2016-2017 Organiser of Geometry and Dynamics Seminar (with Marco Mazzucchelli)
2014-2017 Creator and organiser of Recreative Mathematics Seminar (known as Séminaire de la détente mathématique, more info here.
june 2015 International conference Geometries in action
april 2015 International conference Knots and links in fluid flows
january 2014 International conference Attractors, foliations and limit cycles
Conferences invited talks
november 2013 Young researcher meeting in geometry and dynamics, CIRM, Marseille january 2016 Geometric aspects of modern dynamics, Porto
november 2017 Zero Entropy system, CIRM, Marseille
juin 2018 Teichmüller dynamics, mapping class groups and applications, Institut Fourier, Grenoble
seminars invited talks
Dijon (11/15), Nice (02/16), UFF Rio de Janeiro (05/16), PUC Rio de Janeiro (05/16), Paris Sud (06/16), Avignon (06/16), NRU HSE Nizhny Novgorod (09/16), Rennes (11/16, 09/17), ENS de Lyon (01/17), Marseille (01/17, 09/17), Grenoble (01/17), Paris 13 (03/17), Bordeaux (03/17), Avignon (04/17), Luxembourg(05/17), Lille (11/17), NRU HSE Moscow (12/17), Amiens (04/18), and others...
scientific sejourns
december 2012 ENS de Lyon (invited by Alexey Glutsyuk)
april-may 2016 Instituto Nacional de Matemática Pura e Aplicada, Rio de Janeiro
Languages
Russian is my native language, I am fluent in English and in French.
I have some basic knowledge of German, Spanish and Portuguese.
A complete up-to-date CV is available upon request, the last (updated on August 2018) version is available on the drive, in French.